Transformation Matrices and Spaces. Linear Algebra 101 in Unity

These are important concepts to understand to create and modify visual items in Unity. I created this article as a introduction for advanced topics.

This is made for beginners, trying to avoid technical concepts and simplifying very much the maths.

What is a space?

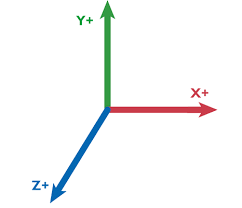
It can be a very complex definition and there are many types of spaces. (As complex as this). In our case, we just care about what space means inside Unity. Our space is defined by the mix of an origin point plus a definition of the axis, both conform the Cartesian Coordinate System. There is always one origin. In 3d, there are 3 axes pointing at different directions. In 2D there are 2 pointing at two different directions. But in our space, all of the axis have 90 degrees from each other. That will make things easier.

Some 3d engines have Z looking up, others have y, they define the space differently.

Any point or vector expressed in that space will have to define a value for each axis. That way we know where he point is / vector points at.

What is world space? 

World space is a common place for all 3d engines. Origin in the 0,0,0 of your Unity scene and with those x,y,z axes it draws by default in those positions.  This is the default world space in Unity, with the origin in 0,0,0 of the world.

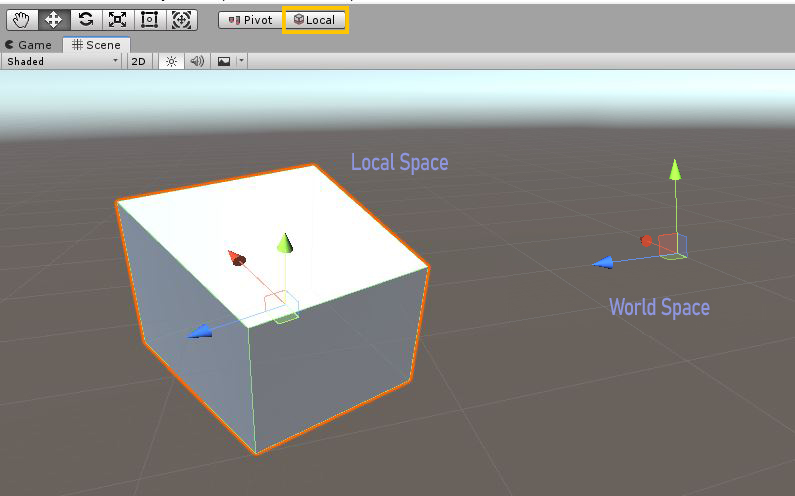
What is local space? 

Each gameObject contains its local space, because it is local to the object you are talking about. It is the space defined by the Transform component of that object. You can view the axis in local space of the selected object by changing to local space view in the Scene View on top.

You will see that if you turn the object around, the axes will turn also. Instead, the world space is always stays the same (although it is painted in the center of the selected object for convenience, think that it should be on the 0,0,0 of the world).

What is expressing a vector in another space?

If you have vector A in world space and you have another object B which has a local space, defined by the transform of the object (GameObject.transform). 

If you want to express the vector A in world space relative to that B object, you have to apply a transformation from world space to the local space of B. 

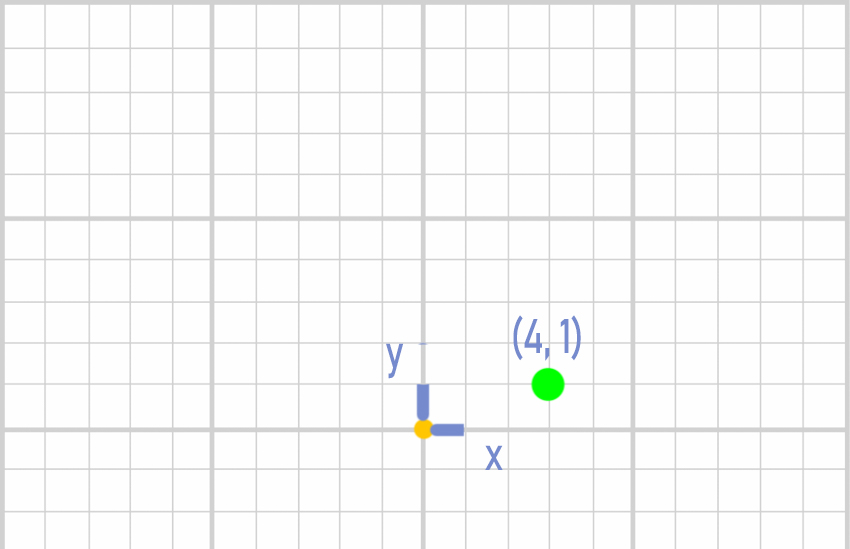
This is vector A expressed in world space. In world space that vector that goes from (0,0) to (4,1) or the point (4,1) (both are the same result but different concepts).

And now you want to express that point/vector local to the object B. The object B defines that Space where X and Y are pointing to different directions. What coordinates has that green point now?

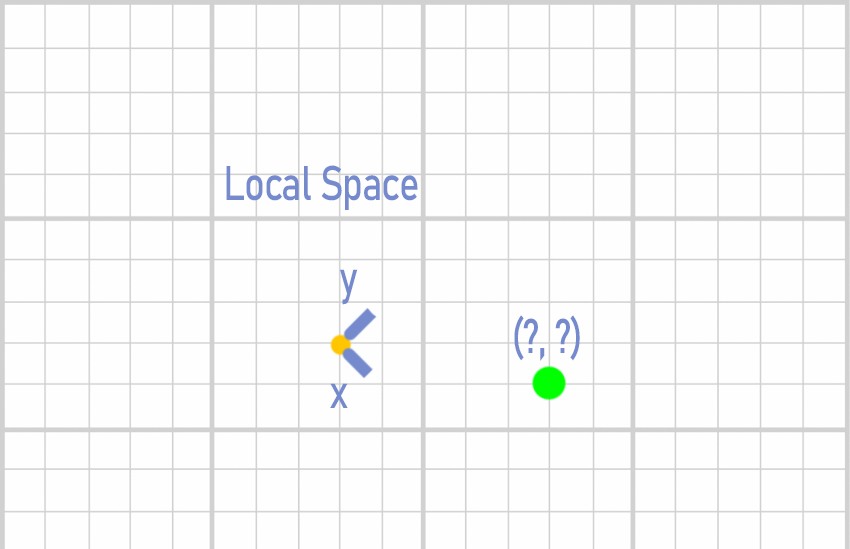
To do this, you take vector A  (4,1) from world space and tranfsorm it to the local space of B. We will talk about how to do these operations in Unity later on.

This is very useful, but probably you don't still see where. I had the same problem when I learned this in highschool. Right now I just use it everyday.  This is what is called a "base change", "base switch", "world to local transformation"...

You can do this from ANY space to ANY space, not only World to local and viceversa.

What is a transformation matrix?

You can use it to perform a transformation from one space to another. You take the Transform Component from the object that defines the space, and get the transform.worldToLocalMatrix and multiply it by the vector in world space or transform.localToWorldMatrix and multiply it by a vector in local space depending on the vector you are giving and in which space you want to express as a result.

But it will help if you use these methods given by the Matrix4x4 class when you get those matrices: MultiplyPoint" or "MultiplyVector". It will return the vector in the other space.

Matrices are just a mix of values, you probably studied that in school. But transformation matrices have this special configuration:

The blue part contains the rotation and scale. The red part contains the translation. m44 is always 1. The green part  normally has 0s unless it is a transformation that performs a "shear" operation, which means you are changing the perspective and those weird operations that you maybe use some day.

Don't worry about what values are inside the matrix, you don't need to know, unless you want to read more about it. 

If you are worried about the performance of each operation, since there are many ways to do this, and many functions, not only in Matrix4x4, but inside Transfrom class (Transform.TransformPoint, TransformVector, TransformDirection...). What's the difference?

Here's another article to help you choose between different methods.